学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとうございます。 開設以来、多くの皆様にご利用いただいております本ブログは、 より皆様のお役に立てるよう、2020年10月30日より形を変えてリニューアルします。 以下、弊社本部サイト『受験対策情報』にて記事を掲載していくこととなりました。 『受験対策情報』https://www.sakusakura.jp/examination/ 『受験対策情報』では、中学受験/高校受験/大学受験に役立つ情報、 その他、勉強に役立つ豆知識を掲載してまいります。 ぜひご閲覧くださいませ。今後とも宜しくお願い申し上げます。 |
こんにちは、サクラサクセスです。
このブログでは、サクラサクセスの本物の先生が授業を行います!
登場する先生に勉強の相談をすることも出来ます!
"ブログだけでは物足りない"と感じたあなた!!
ぜひ無料体験・相談をして実際に先生に教えてもらいませんか?
さて、そろそろさくらっこ君と先生の授業が始まるようです♪
今日も元気にスタート~!
田庭先生
数学担当の田庭です。
10連休はいかがでしたか?
旅行・部活・帰省など様々な過ごし方ができたでしょうか?
10連休が終わればいよいよ中間テストです。
元号の切り替えと同様に勉強モードに切り替えてテストに向けて頑張っていきましょう。

10連休はしっかり休んだから、次はテスト勉強しなきゃね!
頑張るぞ~!!
塾選びで悩んでいませんか?
「情報収集」「比較検討」「お子様との相性」が大切と分かっていても、難しいですよね。
サクラサクセスは島根県・鳥取県・滋賀県・佐賀県にある地域密着型の個別指導塾です。
そんな悩める保護者様へ、公式LINEで特別なコンテンツをご用意しました!
- 無料体験詳細 - LINEで無料体験の予約が可能!
- オペレーターに質問 - チャットで疑問に思ったことを相談できる!
- 講習詳細 - 模試や季節講習の情報も充実!
- 塾比較資料 - 様々な塾を比較検討できる!
- 料金シミュレーション - 学年毎の費用がすぐ分かる!
さらに、個別指導塾だからできる、お子様の個性と目標に合わせた学習プランもご提案!
多くの生徒を志望校合格へ導いたサクラサクセスが、あなたの塾選びを全力でサポートします!
今すぐ、最適な塾選びの一歩を踏み出しましょう!
※特典は予告なく変更となる場合があります。
※悪質なメッセージには対応いたしかねますので、予めご了承ください。
愛知県で塾をお探しなら、Jアカデミアにご相談ください!
「愛知県の入試情報や、うちの子の学校に合った対策をしてほしい…」
Jアカデミアは、地元愛知県(名古屋市・尾張旭市・長久手市・瀬戸市・みよし市・豊明市)のお子様の学習を長年サポートしてきた個別指導塾です。
地域の中学校ごとの進度やテスト範囲に合わせた対策はもちろん、入塾テストなしで、どんな学力のお子さまも歓迎。
一人ひとりに合わせた個別カリキュラムで、無理なく着実にステップアップできます。
\ 愛知県のお子様に選ばれる理由 /
- 成績向上率70%超の確かな実績
- 地域中学の情報に精通し、学校別対策ができる
- 一人ひとりに合わせた個別最適カリキュラム
- 定期テスト前は無料補習を徹底サポート
- 生徒に寄り添う質問しやすい雰囲気
まずは、無料体験でお子様との相性や教室の雰囲気をご確認ください。
▼実際の授業を見てみたい方はこちら
▼コースや料金を詳しく知りたい方はこちら
地元密着だからこそできる、愛知県の教育事情に合わせた具体的なアドバイスもご好評いただいています!
0の発見
田庭先生
新元号が「令和」という事で今回は最初に零(0)について少し話をします。
(ややこじつけ感が出ていますがご容赦ください)
数字自体は古代エジプトや古代ローマでも使用されていましたが、
その時には0という数字はありませんでした。
数字は量をあらわすものなので必要とされなかったのでしょう。
普段の生活ではこの感覚はなんとなく分かるのではないでしょうか?
「冷蔵庫に牛乳が1パック残っている」という表現は使いますが、
「冷蔵庫に牛乳が0パック残っている」とは言わず
「冷蔵庫に牛乳がない」と言いますよね。
しかし、
今からおよそ1300~1400年前のインドでこの「ない」「無」という数字0が発見されました。
この0の発見により、
あらゆる数を簡単に分かりやすく表現する事ができるようになりました。
例えばローマ数字では0がありませんから、
1、2、3、4、10、20、30、40は別物として表す必要があります。
ローマ数字
1→Ⅰ 10→Ⅹ
2→Ⅱ 20→XX
3→Ⅲ 30→XXX
4→Ⅳ 40→XL
田庭先生
といった形です。
気になる方はインターネットでローマ数字を検索していただければ分かると思いますが、
まず数字を覚えるだけで一苦労です。

0という考え方がないだけで、こんなにも規則性が違うんだね・・・!
田庭先生
その他にも0の発見により多くの数学の進化が実現されました。
難しい話になるので気になる方は高校・大学で勉強したり自分で調べてみたりして下さい。
正負の計算
田庭先生
今日の学習のテーマは正負の計算です。
中学に入学して初めて習う正負の数ですが、
ここでつまずくと、
この後の中学・高校での数学が非常に難しくなるので、
しっかり理解をしておいて下さい。
まず理解してほしい事が符号(数字の前の+、-)です。
これはその数が0より大きいか小さいかを示しています。
分かりやすく言えば数直線で0の左側か右側かという事です。
+3なら0より3つ右、-6なら0より6つ左という事です。
分かりにくければまずは、3歩右や6歩左と言った風に考えると分かりやすいと思います。
次に正負の計算ですが、
ここで重要な事は
計算式に出てくる+、-は加法・減法を表す記号だという事です。
符号の+、-とは別物です。
ここをしっかり理解しておきましょう。
加法
加法とは足し算、言い換えれば「そのまま進める」という事です。
(-2)+(-5)であれば
「(-2)」;2歩左
「+」;そのまま進める
「(-5)」;5歩左
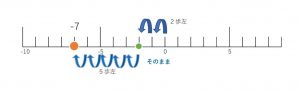
という事で答えは「-7」
減法
減法とは引き算。言い換えれば「逆に進める」という事です。
(-6)-(-12)であれば
「(-6)」;6歩左
「-」;逆に進める
「(-12)」;12歩左
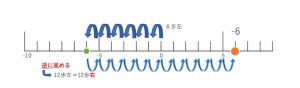
という事で答えは「+6」
まとめ
○数字の前の(+、-)は、
その数字がどこに(0より右か左か)いるかを表す記号。
○数字と数字の間の(+、-)は、
加法、減法(そのまま進めるか、逆に進めるか)を表す記号。
田庭先生
ここを混同せずに理解しておいて、数直線で考えればミスなく解けるはずです。
数直線の作図は毎回描かなくても大丈夫です。
はじめは面倒かもしれませんが繰り返しすれば頭の中でできるようになり、
さらに繰り返せば、数直線の考え方を通さなくても自然とできるようになるはずです。
あとは訓練です。
問題を解いた量がものを言うのでここは演習を重ねて下さい。
繰り返しになりますがこの正負の数の計算でつまずくと今後の数学でとても苦労します。
絶対にマスターしておいて下さい。

今後の数学でつまづかないためにも、
符号の考え方に注意して、問題を繰り返し解いてみる!
ありがとうございました!!
最後までお読みくださりありがとうございます♪
実際に、このブログに登場した先生に勉強の相談をすることも出来ます!
「ブログだけでは物足りない」、「もっと先生に色々教えてほしい!」と感じたあなた、
ぜひ無料体験・相談をして実際に先生に教えてもらいましょう!
友だちも誘って、ぜひ一度体験しに来てくださいね!



